摘 要:北京奧運(yùn)會(huì)大興排練場大跨度交叉威亞主鋼索網(wǎng)是奧運(yùn)會(huì)、殘奧會(huì)開閉幕式上空演員、道具訓(xùn)練的承載基礎(chǔ),其受力性能對(duì)上空設(shè)備的安全至關(guān)重要。采用理論分析和數(shù)值計(jì)算相結(jié)合的方法,運(yùn)用ANSYS和EASY程序,對(duì)奧運(yùn)會(huì)排練場上空鋼索網(wǎng)的受力特性進(jìn)行了分析。結(jié)果表明,南北單索的最大內(nèi)力值115.54kN。交叉鋼索網(wǎng)是一個(gè)內(nèi)力重新分配能力很強(qiáng)的自適用體系,最大拉力90.63kN。大跨度交叉鋼索網(wǎng)結(jié)構(gòu)受力合理,安全可靠。
關(guān)鍵詞:威亞鋼索網(wǎng);找形;非線性分析;有限元;力密度法
北京奧運(yùn)會(huì)大興排練場是為解決奧運(yùn)會(huì)、殘奧會(huì)開閉幕式演員、道具的排練和威亞系統(tǒng)考核、調(diào)試建造的。排練場建有模擬國家體育場內(nèi)環(huán)高度的鋼桁架柱,并在其上建有一個(gè)大跨度交叉鋼索網(wǎng),用來承載威亞,模擬訓(xùn)練四個(gè)儀式空中演員、道具的演練。因此,上空鋼索網(wǎng)體系的受力性能對(duì)于演員和設(shè)備的安全至關(guān)重要。本文對(duì)奧運(yùn)會(huì)排練場上空交叉鋼索網(wǎng)的受力特性進(jìn)行了計(jì)算和分析,為設(shè)計(jì)提供依據(jù)。
1 索網(wǎng)體系及受力特點(diǎn)
1.1 索網(wǎng)體系
奧運(yùn)會(huì)排練場上空鋼索布置如圖1所示,是一個(gè)由多根放射狀索和鋼管組成的索網(wǎng)體系,共有18根承載鋼索。南北向2根通長承載鋼索,南北向不通長鋼索2根,跨度184m;東西向不通長鋼索14根,跨度126m。東西向和南北向16根不通長鋼索通過空中一根長13.4m的鋼管連接起來,呈放射狀布置。鋼索上設(shè)置了荷載為500kg、200kg、100kg三種威亞裝置,用于開閉幕式上空演員、道具排練。這種形式的鋼索網(wǎng)空間結(jié)構(gòu)在國內(nèi)外尚屬首例。
上空鋼索參數(shù)如下:鋼絲繩為6×19S+IWR,公稱直徑32mm,表面鋼絲直徑≥1.5mm,重量4.15kg/m,公稱抗拉強(qiáng)度1870MPa,鋼絲繩最小破斷力632kN。彈性模量6.86×1010Pa,泊松比0.30。中心鋼管直徑426mm,壁厚20mm,長13.4m,重43.43kN,密度7850kg/m3,彈性模量2.1×1011Pa。
計(jì)算分析時(shí),不考慮拉向地面的斜向鋼索,直接從柱頂點(diǎn)開始向中心鋼管建模。鋼絲繩計(jì)算金屬面積530mm2,計(jì)算重量5.15kg/m(其中1kg為附加在鋼索上威亞牽引繩的重量)。
1.2 荷載工況
荷載包括:鋼索、中心鋼管、威亞自重,演員、道具重量,溫度荷載等。由于荷載工況組合繁多,本文僅對(duì)控制工況進(jìn)行計(jì)算。控制工況分上空索網(wǎng)工況和南北單索工況兩部分,分別見表1、表2。
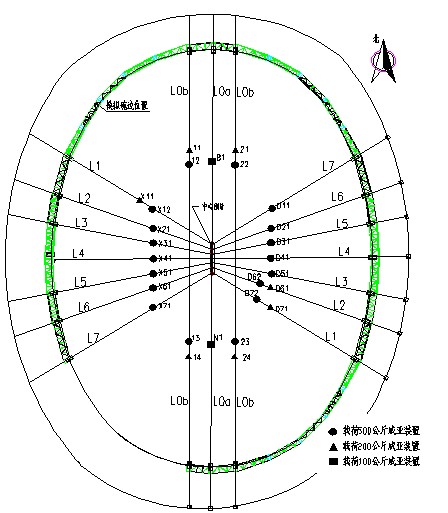

圖1 排練場上空鋼索網(wǎng)及威亞布置圖
表1 上空鋼索網(wǎng)計(jì)算工況
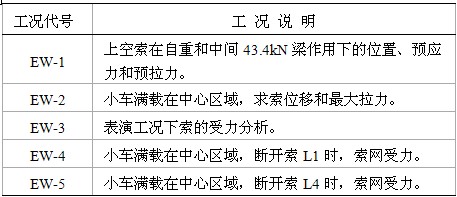
表2 上空南北通長鋼索計(jì)算工況

2 索網(wǎng)計(jì)算模型
2.1索網(wǎng)找形理論
由于索在無應(yīng)力情況下沒有剛度,不具有承載力和一定的形狀,所以必須施加適當(dāng)?shù)念A(yù)應(yīng)力來使其產(chǎn)生足夠的剛度并確定形狀。索網(wǎng)結(jié)構(gòu)的形態(tài)確定是一個(gè)典型的幾何非線性大位移問題,幾何外形的微小變化都會(huì)引起結(jié)構(gòu)性能的較大變化。幾何外形、所承受的外荷載和內(nèi)應(yīng)力三者之間以非線性方式相互作用和影響。因此,其工作階段的幾何狀態(tài)一般是難以在事先確定的,必須通過找形。找形過程的實(shí)質(zhì)就是通過求解在事先確定的邊界條件下建立的非線性方程組,從而獲得與給定的預(yù)應(yīng)力分布相對(duì)應(yīng)的初始幾何形態(tài)[1]。在此基礎(chǔ)上,再進(jìn)行加載和荷載分析。目前,找形分析主要包括力密度法、動(dòng)力松弛法、基于有限元分析的節(jié)點(diǎn)平衡法和支座提升法等[2,3]。
2.1.1 非線性有限元分析
由于索網(wǎng)結(jié)構(gòu)在荷載作用下一般處于小應(yīng)變、大位移狀態(tài),所以該類結(jié)構(gòu)有限元計(jì)算需考慮結(jié)構(gòu)的幾何非線性問題。采用坐標(biāo)列式U. L (Update Lagrange) 方法,根據(jù)虛功原理可得非線性結(jié)構(gòu)在任意時(shí)刻t時(shí),結(jié)構(gòu)變形的增量平衡方程為[4,5]:
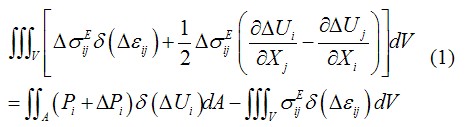
根據(jù)最小勢能原理可建立有限元基本方程,其整體坐標(biāo)系中單元的基本方程為:

為單元的非線性剛度矩陣; 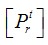 為節(jié)點(diǎn)不平衡力。解這類方程組為加速收斂和減小求解誤差,采用Newton-Raphson方法和增量方法求解較為合適。
為節(jié)點(diǎn)不平衡力。解這類方程組為加速收斂和減小求解誤差,采用Newton-Raphson方法和增量方法求解較為合適。
2.1.2 力密度法
力密度法是由Linkwitz、Schek[6]等提出的一種用于索網(wǎng)結(jié)構(gòu)的找形方法。其基本原理是:將膜結(jié)構(gòu)離散為節(jié)點(diǎn)和桿元組成的索網(wǎng)結(jié)構(gòu)模型,對(duì)每一節(jié)點(diǎn)建立靜力平衡方程,通過預(yù)先給定力密度值,將幾何非線性問題轉(zhuǎn)化為線性問題,聯(lián)立求解一組線性方程組得到索網(wǎng)各節(jié)點(diǎn)的坐標(biāo)。如圖2所示,對(duì)索網(wǎng)中任意節(jié)點(diǎn) ,承受集中力 ,與此節(jié)點(diǎn)相連接的桿元為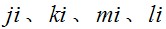 。根據(jù)靜力平衡得方程式:
。根據(jù)靜力平衡得方程式:
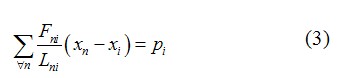
式中:n 為i 點(diǎn)相連的各節(jié)點(diǎn); 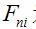 為與i 節(jié)點(diǎn)相鄰的桿元的內(nèi)力;
為與i 節(jié)點(diǎn)相鄰的桿元的內(nèi)力; 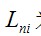 為與i 節(jié)點(diǎn)相鄰的桿元的長度;
為與i 節(jié)點(diǎn)相鄰的桿元的長度;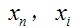 為節(jié)點(diǎn)坐標(biāo)列向量; 為荷載列向量。
為節(jié)點(diǎn)坐標(biāo)列向量; 為荷載列向量。
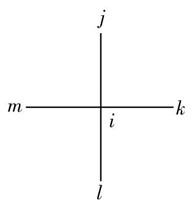
圖2 節(jié)點(diǎn)受力模型圖
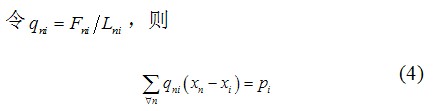
由于力密度法只要求給出離散后結(jié)構(gòu)各桿件的幾何拓?fù)潢P(guān)系、力密度值和邊界節(jié)點(diǎn)坐標(biāo),即可建立關(guān)于節(jié)點(diǎn)坐標(biāo)的線性方程組,并求得節(jié)點(diǎn)的真實(shí)坐標(biāo),避免了初始坐標(biāo)錄入問題和非線性收斂問題,因而計(jì)算速度快,計(jì)算精度也能滿足工程要求。
2.2 索網(wǎng)的找形
索網(wǎng)的找形采用力密度法和基于非線性有限元分析的節(jié)點(diǎn)平衡法。分別采用程序ANSYS和德國索膜軟件EASY
8.0實(shí)現(xiàn)。由于EASY是專業(yè)索膜軟件,索網(wǎng)的找形通過建立模型,輸入?yún)?shù)-找力與結(jié)構(gòu)的平衡關(guān)系-梁單元分析即可實(shí)現(xiàn)。
ANSYS是一個(gè)大型的有限元通用程序,對(duì)索網(wǎng)的找形稍微復(fù)雜,主要計(jì)算步驟如下:先以柱頂點(diǎn)和中心鋼管為控制關(guān)鍵點(diǎn),建立初設(shè)形態(tài)的模型,劃分單元,指定索的材料參數(shù)和初應(yīng)力。然后施加重力荷載,在支座點(diǎn)約束平動(dòng)自由度,考慮大變形與應(yīng)力剛化效應(yīng),采用Full Newton Raphson 法計(jì)算索網(wǎng)結(jié)構(gòu)的初始形態(tài),得到模型在初設(shè)形態(tài)和初始預(yù)應(yīng)力條件下的平衡狀態(tài),將計(jì)算位移結(jié)果采用ANSYS的UPGEOM命令更新結(jié)構(gòu)幾何體型,再進(jìn)行迭代計(jì)算,直到更新體型后計(jì)算的位移差值達(dá)到毫米級(jí)為止,完成找形。由于索網(wǎng)結(jié)構(gòu)工作在彈性階段,因此有限元分析時(shí),不考慮結(jié)構(gòu)材料的非線性,僅考慮幾何非線性的影響。
3 索網(wǎng)受力特點(diǎn)及計(jì)算結(jié)果分析
3.1 有限元法與力密度法結(jié)果的比較
自重下索網(wǎng)的應(yīng)力和變形ANSYS計(jì)算結(jié)果見圖3。表演工況下索網(wǎng)的內(nèi)力和變形EASY計(jì)算結(jié)果見圖4。
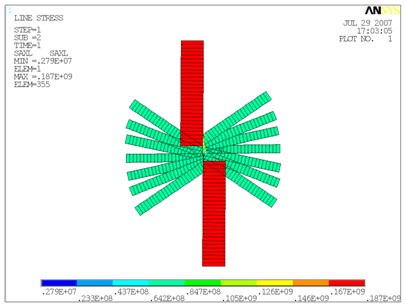
(a) 索網(wǎng)應(yīng)力圖
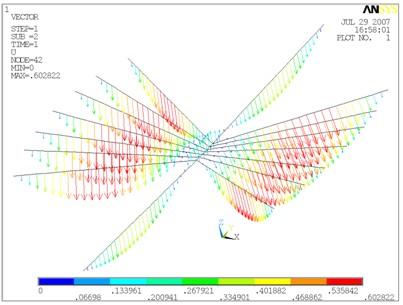
(b)索網(wǎng)相對(duì)初始變形
圖3 自重下索網(wǎng)的應(yīng)力及初始變形
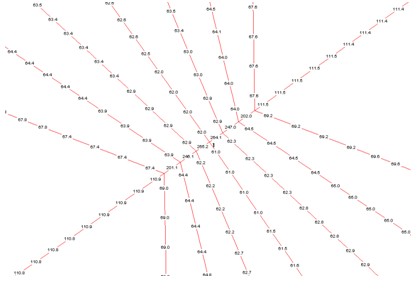
(a) 索網(wǎng)單元及內(nèi)力分布
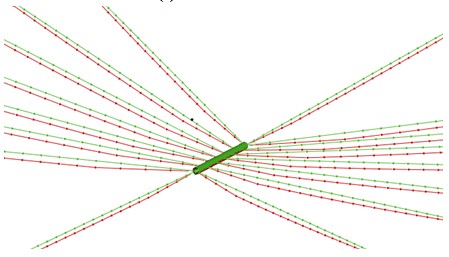
(b)索網(wǎng)變形圖
圖4 表演工況下索網(wǎng)的內(nèi)力及變形
3和表4分別是自重和表演工況下ANSYS與EASY計(jì)算結(jié)果比較。
表3 自重下索網(wǎng)ANSYS與EASY結(jié)果比較
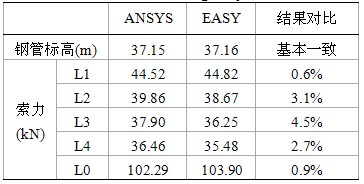
表4 表演工況下ANSYS與EASY結(jié)果比較
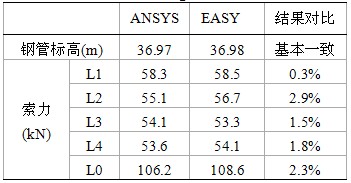
從結(jié)果對(duì)比可以看出,兩種方法計(jì)算的結(jié)果基本一致,誤差在5%范圍以內(nèi),說明計(jì)算結(jié)果可信。
3.2 數(shù)值解與理論解的比較
南北單索實(shí)際上就是一個(gè)單跨度的懸索,有理論解。一個(gè)集中荷載的單跨度懸索跨中最大撓度計(jì)算公式為
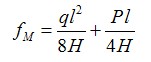 (5)
(5)
式中: 為懸索線荷載,kg; 為懸索跨度,m;l 為懸索集中荷載,kg;H 為懸索張力,kg;fm 為懸索跨中最大撓度,m。
根據(jù)公式(5),得到一個(gè)集中荷載的單跨度懸索張力計(jì)算公式
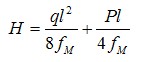 (6)
(6)
南北單索的工況計(jì)算結(jié)果見表5。
表5 ANSYS計(jì)算索拉力與解析解比較
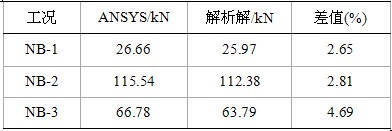
注:單索最小安全系數(shù)=最小破斷力/最大內(nèi)力標(biāo)準(zhǔn)值=5.45
表5表明,ANSYS計(jì)算結(jié)果與解析解相差在5%之內(nèi),說明數(shù)值計(jì)算結(jié)果可信。同時(shí),計(jì)算表明,南北單索的最小安全系數(shù)為5.45。
3.3 交叉鋼索網(wǎng)計(jì)算結(jié)果及分析
在上述驗(yàn)證計(jì)算模型的基礎(chǔ)上,不同工況下索網(wǎng)的受力進(jìn)行了計(jì)算分析。計(jì)算結(jié)果分別見表6和圖5、圖6。
表6 不同工況下索網(wǎng)受力 kN
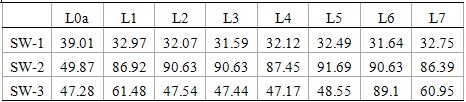
注:①由于索網(wǎng)關(guān)于中心180°旋轉(zhuǎn)對(duì)稱,因此只給出了一半索網(wǎng)的受力;②最小安全系數(shù)=6.89。
從表6可以看出,無論是在自重還是在極限荷載作用下,索網(wǎng)各根鋼索的內(nèi)力大小基本一致。說明上空索網(wǎng)的受力均勻,是一個(gè)內(nèi)力分布均勻、自適用能力很強(qiáng)的自平衡體系。斷開一根索后,整個(gè)索網(wǎng)的內(nèi)力重分布(圖5、圖6)特點(diǎn),更加清楚的說明了這一點(diǎn):斷開鋼索L1后,鋼索L2內(nèi)力最大值126.9kN,鋼索L3內(nèi)力最大值111.4kN,其它鋼索的內(nèi)力值在80~90kN左右;斷開鋼索L4后,鋼索L2、L3、L5、L6內(nèi)力最大值在104kN左右,對(duì)稱7根鋼索的內(nèi)力值有所減小,約84kN左右;說明上空交叉索網(wǎng)結(jié)構(gòu)是一個(gè)內(nèi)力分布均勻、內(nèi)力重新分配調(diào)節(jié)能力很強(qiáng)的自適用平衡體系。上空索網(wǎng)的最小安全系數(shù)為6.89。
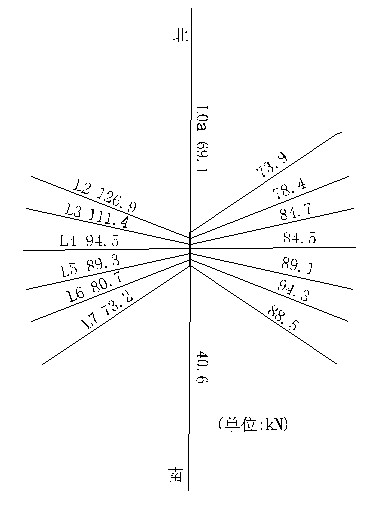
圖5 斷開L1后索網(wǎng)受力
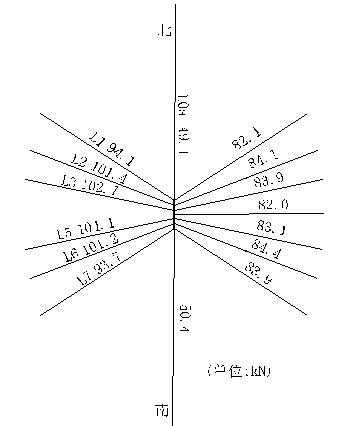
圖6 斷開L4后索網(wǎng)受力
4 結(jié)論
采用理論分析和數(shù)值計(jì)算的方法,利用ANSYS和EASY程序,對(duì)奧運(yùn)會(huì)排練場上空鋼索的受力進(jìn)行了分析。結(jié)果表明,
1)兩種方法的數(shù)值解和理論解析解結(jié)果基本一致,說明數(shù)值計(jì)算結(jié)果真實(shí)、可信。
2)南北單索的最大內(nèi)力值為115.54kN。
3)交叉索網(wǎng)是一個(gè)內(nèi)力重新分配能力很強(qiáng)的自適用體系,最大拉力91.69kN。
4)上空索網(wǎng)結(jié)構(gòu)受力合理,安全可靠。
參考文獻(xiàn)
[1] LI Yang,GAO Ri,YAN Jing-ton.
The influence of form-finding for cable net structures by self-weight [J].
Building Science Research of Sichuan,2003,29(2):29-31 (in Chinese).
[2] XIA Zheng-chun,LI Li,SHI Xiao-wei. Camparison between two methods for form finding of
prestressed cable nets [J]. Journal of Wuhan Urban Construction Institute,2005,22(1):66-69,77 (in Chinese).
[3] ZENG Xiao-fei,YE Ji-hong,YE Ye. Comparisons between
dynamic-relaxation method and force-density method for form finding of
pretensioned cable roofs [J]. Spatial Structures, 2003, 9(4):55-58 (in
Chinese).
[4] Li Renpei. The nonlinear finite element
analysis of cable net structures [D]. Chongqing: College of Civil Engineering
Chongqing University, 2006.
[5] You Guimo, Yao Qian-feng, Shang
Ren-jie,et al. Analysis on bearing behaviors of cable-nets structure with cable
edge [J]. Steel Structures,2006,21(3):72-78 (in Chinese).
[6] Schek H J. The Force Density Method for
Form–Finding and
Computation of General Network[J].Computer Methods in AppliedM echanics and
Engineering,1974,3(2): 115-134.
(總裝備部工程設(shè)計(jì)研究總院,北京 100028)
"歡迎大家轉(zhuǎn)摘!轉(zhuǎn)載須注明中國建筑金屬結(jié)構(gòu)協(xié)會(huì)建筑
鋼結(jié)構(gòu)網(wǎng)(www.fsled.com.cn)謝謝合作!"
![]() 獲獎(jiǎng)鋼結(jié)構(gòu)企業(yè)個(gè)人專訪錄
獲獎(jiǎng)鋼結(jié)構(gòu)企業(yè)個(gè)人專訪錄
![]() 鋼結(jié)構(gòu)行業(yè)產(chǎn)品展銷會(huì)
鋼結(jié)構(gòu)行業(yè)產(chǎn)品展銷會(huì)












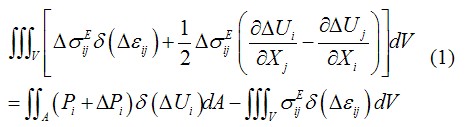

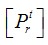
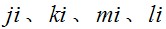
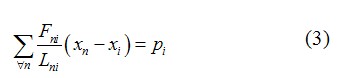
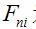
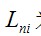
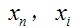
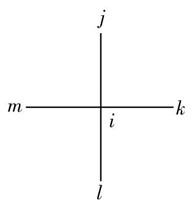
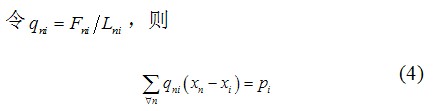






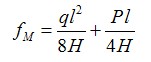 (
(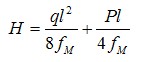 (
(



 :
: 