中國建筑金屬結(jié)構(gòu)協(xié)會
建筑鋼結(jié)構(gòu)分會主辦
摘 要：通過采用有限元軟件對薄壁方鋼管梁柱加腋節(jié)點進行數(shù)值模擬，分析該節(jié)點的性能以及該節(jié)點的破壞模式。結(jié)果表明：該節(jié)點屬于半剛性節(jié)點，不能簡單的視為剛性連接或鉸接；并且加勁肋應(yīng)力變化較大，設(shè)計時應(yīng)具有足夠的厚度；該節(jié)點的最終破壞是由于方鋼管梁的局部屈曲，符合“強節(jié)點弱桿件”的抗震設(shè)計原則。
關(guān)鍵詞：薄壁方鋼管；加腋節(jié)點；半剛性連接；數(shù)值模擬
1前 言
薄壁輕鋼結(jié)構(gòu)作為一種新型的鋼結(jié)構(gòu)體系，由于薄壁輕鋼結(jié)構(gòu)具有整體性好、高次超靜定的結(jié)構(gòu)體系，具有多道抗震防線的優(yōu)點，并且符合我國的環(huán)保、節(jié)能、節(jié)水、住宅產(chǎn)業(yè)化政策，將成為我國建筑發(fā)展的新趨勢[1]。在我國薄壁輕鋼結(jié)構(gòu)房屋體系（圖1）當中，其輕鋼骨架梁柱構(gòu)件通常采用冷彎薄壁方鋼管、矩形鋼管、C型鋼、L型鋼、槽型鋼，然而在這些截面形式當中，以方鋼管、矩形鋼管的截面形式較優(yōu)越。這類截面材料繞中和軸均勻分布，使得截面具有良好的抗壓和抗彎扭承載能力以及較大的剛度[2]，從而降低結(jié)構(gòu)的用鋼量。然而在這類輕鋼骨架之間通常采用直接焊接方式（圖2），采用焊接方式連接，密閉性好，板件凈截面面積不會減小，但在這種節(jié)點反復(fù)焊接過程當中，對節(jié)點部分產(chǎn)生很明顯的初始應(yīng)力，節(jié)點脆性明顯增
圖1 輕鋼結(jié)構(gòu)骨架體系（薄壁方鋼管梁柱加腋節(jié)點）
加，降低節(jié)點的延性，然而節(jié)點是構(gòu)成鋼框架不可
缺少的部分，并且歷次地震，如1985年墨西哥城地震、1994年美國諾斯里齊地震、1995年日本阪神地震，大部分輕鋼建筑都以節(jié)點的破壞而導(dǎo)致建筑的倒塌，因此對這類輕鋼結(jié)構(gòu)的節(jié)點連接應(yīng)受到工程界的廣泛重視[3-4]。為此本文提出在方鋼管梁的上下翼緣增設(shè)加勁肋，以改善節(jié)點的強度和剛度。建立三維空間節(jié)點有限元模型進行分析，探討加腋后節(jié)點的性能及其破壞模式。
2.模型建立
2.1幾何模型
圖3為本文研究節(jié)點的三維視圖，其中方鋼管柱的截面尺寸為120×120×3mm，高度為1200mm，兩個方鋼管柱之間間距為600mm；方鋼管梁1、2截面尺寸為100×100×2mm，其中方鋼管梁1長度700mm，方鋼管梁2長度為480mm；加勁板尺寸為120×50×3mm，加勁肋尺寸為40×3mm。
圖2現(xiàn)場焊接節(jié)點（薄壁方鋼管梁柱加腋節(jié)點）
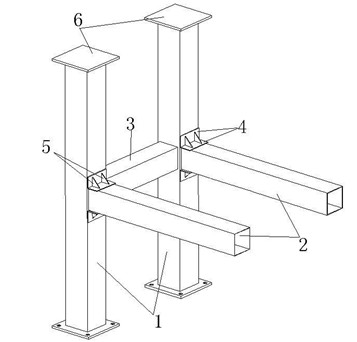
(1-方鋼管柱，2-方鋼管梁1,3-方鋼管梁2,
4-加勁板，5-加勁肋，6-方鋼管柱底板)
圖3 加腋節(jié)點三維視圖
2.2 材料模型
方鋼管梁柱的材料特性見圖5，加勁肋與梁柱所用材料相同，故取相同值。采用多線性材料模型，彈性模量E=161249.7MPa，泊松比ν=0.3。模型采用的屈服準則為Von Mises屈服準則,并且認為材料是各向同性強化的。
2.3有限元模型
采用ANSYS軟件對圖3所示的連接節(jié)點建立有限元計算模型。由于方鋼管梁柱的長度及寬度與其壁厚的比值較大，故采用每個節(jié)點具有6個自由度的殼單元shell181，該單元具有應(yīng)力剛化及大變形功能，具有強大的非線性功能；增設(shè)的加勁肋采用四面體單元solid92，每個節(jié)點具有三個自由度，該單元支持塑性、蠕動、膨脹、應(yīng)力鋼化、大變形和大張力；方鋼管柱上下底板采用solid45單元，并且假定其為剛性；在方鋼管梁1端部增加端板，其中線距離方鋼管柱翼緣距離為650mm，假定其為剛性。對于體單元與殼單元的公共邊界采用共用節(jié)點，建立該節(jié)點的有限元模型如圖4所示，并對節(jié)點域處的單元網(wǎng)格劃分加密。方鋼管柱底部為固端上部為鉸接的邊界條件。
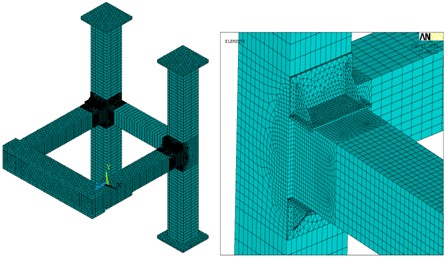
圖4 加腋節(jié)點有限元模型（薄壁方鋼管梁柱加腋節(jié)點）
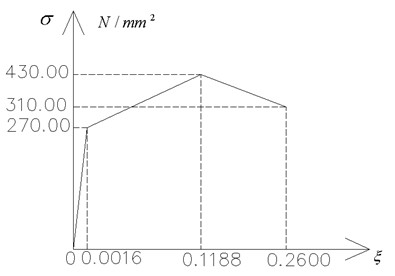
圖5材料本構(gòu)
3.計算結(jié)果分析
3.1荷載位移曲線
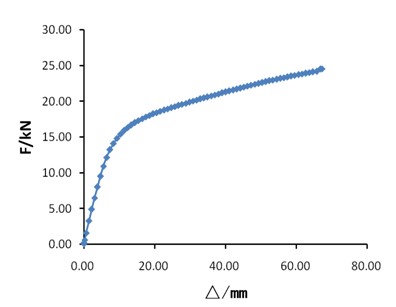
圖6 荷載位移曲線（薄壁方鋼管梁柱加腋節(jié)點）
圖6為該節(jié)點的荷載位移曲線，該節(jié)點在開始處于彈性階段，荷載與位移呈線性增加，當荷載達到13.23kN時，節(jié)點開始屈服，對應(yīng)的屈服位移為7.4mm；隨即進入屈服階段，達到節(jié)點的極限承載力為25.53kN，按全截面塑性發(fā)展，可計算其極限承載力為26.33kN，略大于有限元計算結(jié)果。該節(jié)點的彎矩轉(zhuǎn)角曲線與荷載位移曲線變化相似，同時可計算其初始轉(zhuǎn)動剛度為847.5kN•m。
根據(jù)文獻5當中連接的初始轉(zhuǎn)動剛度Ki標準定義為：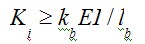
，則為剛接；
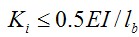，則為鉸接； 
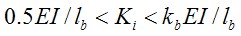，則為半剛性連接；
E為鋼材彈性模量，Ib為梁截面慣性矩，Lb為梁跨度，kb=8（有支撐框架）或kb=25（無支撐框架）。
可計算得：
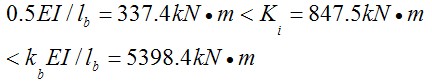即屬于半剛性連接。
當以連接的受彎承載力為標準定義：該節(jié)點的塑性彎矩為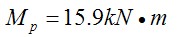 
；粱端的塑性轉(zhuǎn)角： 
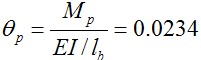。其中取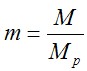 
，
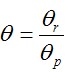，可得其相對彎矩轉(zhuǎn)角曲線如圖7所示，可見該節(jié)點的相對彎矩轉(zhuǎn)角曲線位于半剛性連接區(qū)域類，并且與剛性連接或鉸接連接均相差較大，因此在設(shè)計時不能簡單的將該類節(jié)點視為剛接或鉸接連接。
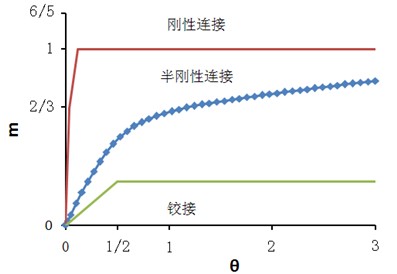
圖7 相對彎矩轉(zhuǎn)角曲線
3.2 應(yīng)力分析
圖8（彈性階段）及圖9（極限荷載作用時）為節(jié)點沿方鋼管梁1長度方向各截面的應(yīng)力發(fā)展趨勢，1.0H、1.5H、2.0H、4.0H（梁形心與柱翼緣交點為坐標原點，X軸、Y軸和Z軸分別為梁寬方向、梁高方向、梁長方向，H為梁截面高度）。
從圖8（a）可以看出梁的彎曲應(yīng)力大致成三角形分布，剪應(yīng)力大致呈拋物線分布，并且各截面處梁腹板的剪應(yīng)力大致相等，均符合經(jīng)典的梁理論。Mises應(yīng)力分布大致也成拋物線型分布，但隨著距離方鋼管柱表面距離的減小，其應(yīng)力變化更大。
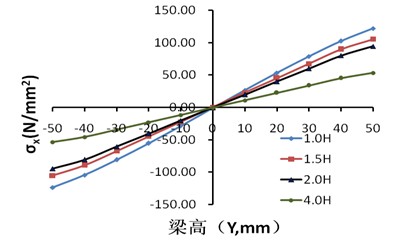
（a）正應(yīng)力分布
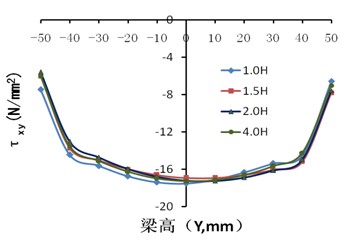
（b）剪應(yīng)力分布
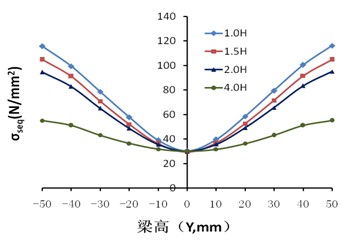
（c）Misses應(yīng)力分布
圖8 沿梁長度方向各截面的應(yīng)力分布圖
從圖9（a）可以看出，正應(yīng)力的分布與彈性節(jié)點變化相似，而剪應(yīng)力與彈性階段的明顯不同，其原因主要是方鋼管梁在進入屈服階段過程中，剪應(yīng)力發(fā)生了內(nèi)力重分布。在X=1.0H時，腹板中部的Mises略大于其余部位，表面在繼續(xù)承受荷載作用時，該部位率先發(fā)生屈曲。
圖10為極限荷載作用下方鋼管柱的Mises應(yīng)力分布，從中可以看出，方鋼管柱腹板應(yīng)力大部分小于屈服應(yīng)力，表明增設(shè)加勁肋能夠明顯改善在節(jié)點域柱腹板的應(yīng)力，防止柱發(fā)生屈曲；圖11為加勁肋與加勁板的Mises應(yīng)力分布，在加勁肋的角部產(chǎn)生應(yīng)力集中現(xiàn)象，局部應(yīng)力已明顯超過屈服應(yīng)力，局部接近極限應(yīng)力值，可見在設(shè)計時三角形加勁肋應(yīng)具有足夠的厚度，以防止應(yīng)力集中而被拉裂。
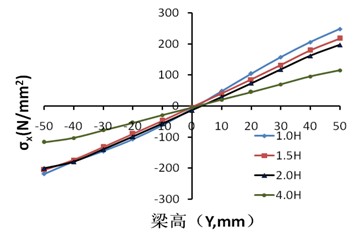
（a）正應(yīng)力分布
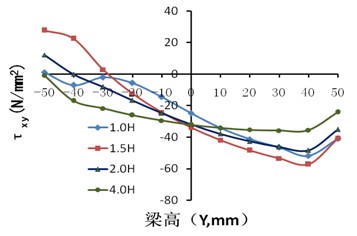
（b）剪應(yīng)力分布
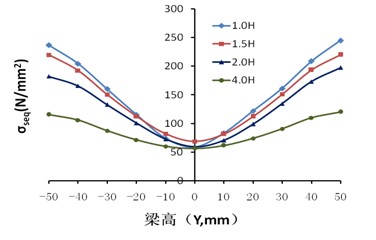
（c）Misses應(yīng)力分布
圖9 沿梁長度方向各截面的應(yīng)力分布圖
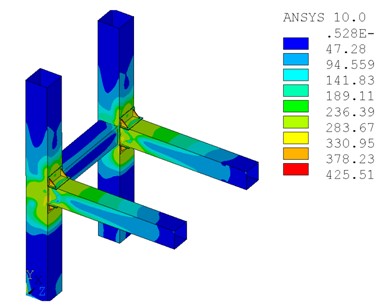
圖10 方鋼管柱的Mises應(yīng)力分布
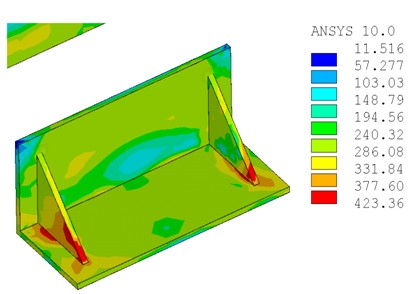
圖11 三角形加勁肋的Mises應(yīng)力分布
3.3破壞模式
節(jié)點在彈性工作狀態(tài)下，荷載位移曲線為基本直線段，荷載隨位移的增大而增長很快，此時連接剛度大，在節(jié)點進入屈服階段之前，加勁肋的應(yīng)力較大，此處也是最早出現(xiàn)塑性區(qū)，隨著荷載的增加，節(jié)點整體荷載位移曲線開始彎曲。隨著荷載的增大，角鋼的塑性區(qū)不斷擴大，剛度下降，加載點位移增加較快，但此時角鋼并沒出現(xiàn)較明顯的屈曲。達到極限荷載后，加勁肋開始出現(xiàn)屈曲，不過此時節(jié)點域處方鋼管梁應(yīng)力增長較快，大部分進入塑性，同時腹板出現(xiàn)向外鼓曲，下翼緣向內(nèi)凹陷（圖12），其變形速度較加勁肋快許多，而此時方鋼管柱的應(yīng)力幾乎沒變，可見該節(jié)點符合“強柱弱梁”的設(shè)計原則。
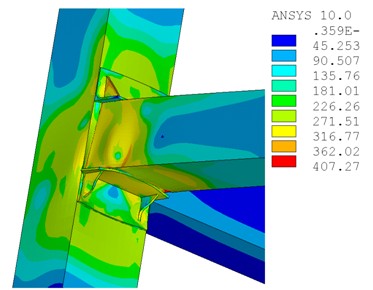
圖12節(jié)點破壞模式
4.結(jié) 論
1）通過對該節(jié)點的荷載位移曲線以及節(jié)點的初始轉(zhuǎn)動剛度大小的研究表明，該節(jié)點既不能簡化成剛性連接，更不能視為鉸接，而屬于梁柱半剛性連接；
2）在外荷載作用下，增設(shè)加勁肋能明顯改善節(jié)點域柱腹板的應(yīng)力，并且節(jié)點的最終破壞模式是由于方鋼管梁的局部屈曲，符合“強節(jié)點弱桿件”的設(shè)計原則。加勁肋的應(yīng)力較大，設(shè)計時應(yīng)具有足夠的厚度，以滿足“強節(jié)點弱桿件”的抗震設(shè)計原則。
參考文獻
[1] 姚勇,褚云朋,鄧勇軍,等.低層冷彎薄壁型鋼結(jié)構(gòu)體系動靜性能數(shù)值模擬[J].建筑結(jié)構(gòu).2011(2):41-45.
[2] 陳驥.鋼結(jié)構(gòu)穩(wěn)定理論與設(shè)計[M].西安建筑科技大學(xué).2005:242-298.
[3] 田俊杰.輕型鋼結(jié)構(gòu)體系節(jié)點半剛性連接性能及框架極限承載力分析[D].長沙理工大學(xué)碩士學(xué)位論文.2003.
[4] 陳堅.新型輕鋼龍骨體系梁－柱節(jié)點試驗性研究及有限元分析[D].武漢理工大學(xué)碩士學(xué)位論文.2006.
[5] 李國強,石文龍,王靜峰.半剛性連接鋼框架結(jié)構(gòu)設(shè)計[M].中國建筑工業(yè)出版社.2009:1-2.
(西南科技大學(xué)土木工程與建筑學(xué)院)
|
： 
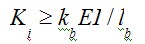
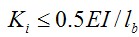
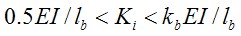
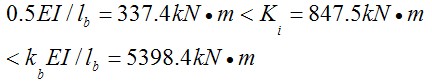
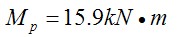
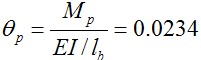
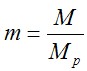
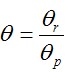